반응형
Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 오버로딩
- localtime
- 멀티태스킹
- 백트래킹
- spring security 설정
- over()
- SQL Mapper
- 둘만의 암호 자바
- CPU
- 자바의 정석
- 입출력
- 리눅스
- 둘만의 암호
- BFS
- 멀티프로세싱
- StringBuffer
- 티스토리챌린지
- 프로그래머스 둘만의 암호
- hackerrank
- 혼공얄코
- 오버라이딩
- spring security
- 오블완
- 다형성
- java
- LocalDate
- 자바의정석
- 캡슐화
- StringBuilder
- 프로그래머스
Archives
- Today
- Total
쉽게 쉽게
[Java/알고리즘] 시간복잡도 계산 본문
반응형
▤ 목차
1. 시간 복잡도란?
알고리즘이 실행될 때 필요한 입력 값과 연산 수행 시간에 따라 효율적인 알고리즘을 나타내는 척도를 의미한다.
시간 복잡도는 빅오 표기법(Big-O notation)을 통해 표현하며, 수치가 작을수록 효율적인 알고리즘을 의미한다.
1. 시간 복잡도 비교 (효율성 순서)
빅오 표기법(Big-O notation)
O(1) < O(log n) < O(n) < O(n log n) < O(n^2) < O(2^n)
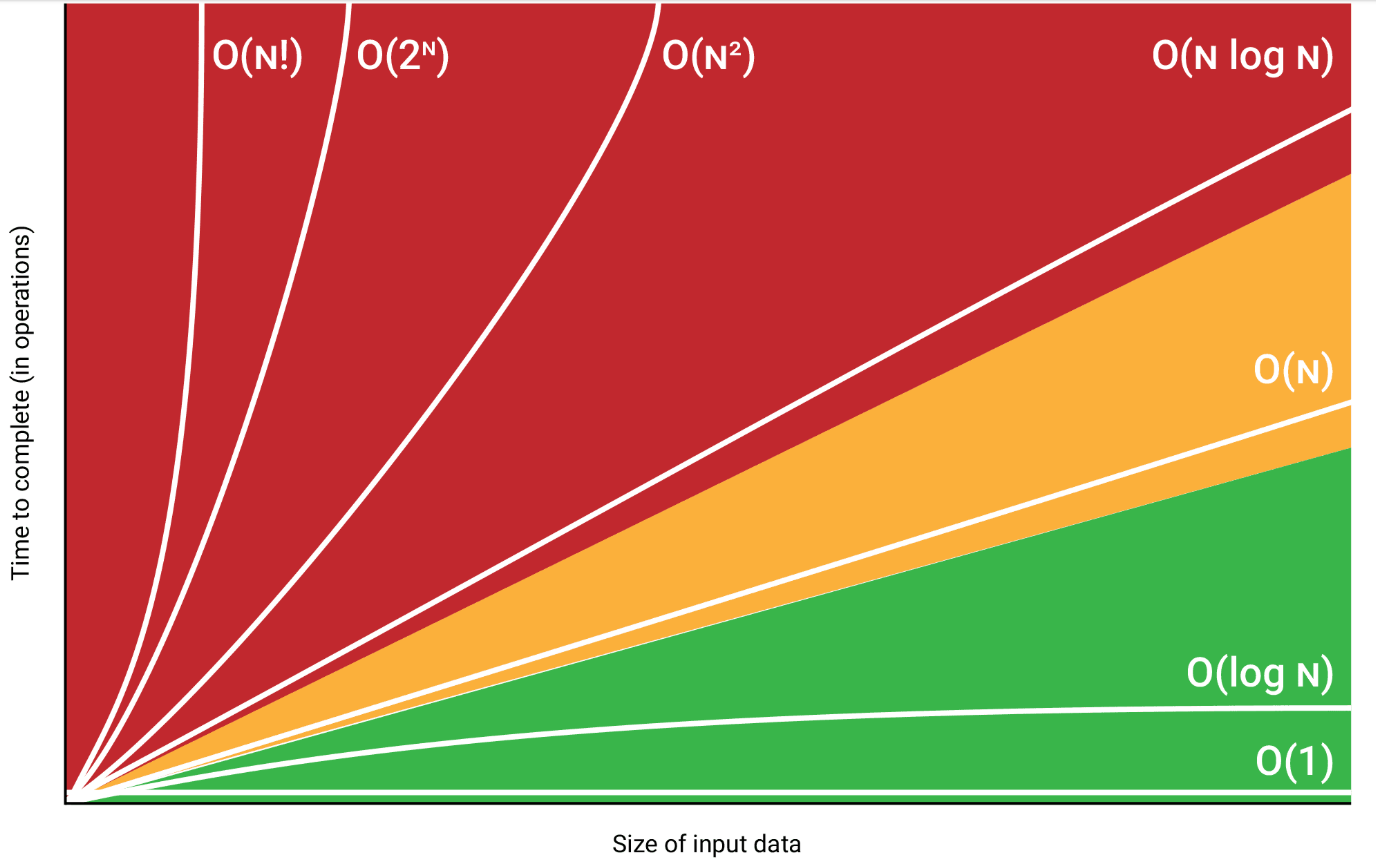
2. 시간 복잡도 계산 방법 (적은 시간 순서)
단순 산술 연산 < 절반씩 줄어들 때 < 단일 반복문 < 정렬 알고리즘 < 이중 반복문 < 재귀
즉 시간 복잡도의 최종 계산은 여러 단계로 나누어진 코드 중 가장 영향력이 큰 부분이 시간 복잡도가 된다.
추가적으로 알고리즘 문제의 제한 시간을 통해 어떤 알고리즘을 구상해야 할지 확인해 볼 수 있다.
보통 1초에 약 1억 번(10^8)의 연산이 가능하다고 가정한다.
- n = 10,000 일 때는 O(n^2) 알고리즘까지 가능하다. (10^8)
- n = 1,000,000일 때는 O(n log n) 이하 알고리즘 필요하다.
2. 시간복잡도 예시
1. O(1) : 상수 시간 (Constant Time)
입력 데이터의 양과 상관없이 언제나 일정한 시간이 걸리는 경우
public void element(int[] arr) {
// 배열의 크기가 10이든 100이든, 0번째를 찾는 속도는 동일
System.out.println(arr[0]);
}2. O(log n) : 로그 시간 (Logarithmic Time)
문제를 해결할 때마다 탐색 범위가 절반씩 줄어드는 경우
대표적으로 이진 탐색(Binary Search)이 있다.
public int binarySearch(int[] arr, int target) {
int left = 0, right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) return mid;
if (arr[mid] < target) left = mid + 1; // 절반 버림
else right = mid - 1; // 절반 버림
}
return -1;
}3. O(n) : 선형 시간 (Linear Time)
입력값 n이 커질수록 수행 시간도 정비례해서 늘어나는 경우
대표적으로 단순 반복문이 있다.
public void elements(int[] arr) {
// n개의 요소를 모두 한 번씩 훑습니다.
for (int i = 0; i < arr.length; i++) {
System.out.println(arr[i]);
}
}4. O(n log n) : 선형 로그 시간 (Linearithmic Time)
효율적인 정렬 알고리즘들이 이에 해당된다.
대표적으로 Arrays.sort(), 병합 정렬(Merge Sort), 퀵 정렬(Quick Sort)이 있다.
// 예: 병합 정렬(Merge Sort)
public void mergeSort(int[] arr, int left, int right) {
if (left < right) {
// 1. 반으로 나눈다 (이 과정이 반복되어 log n 층을 만듦)
int mid = (left + right) / 2;
mergeSort(arr, left, mid); // 왼쪽 반 쪼개기
mergeSort(arr, mid + 1, right); // 오른쪽 반 쪼개기
// 2. 합친다 (각 층마다 전체 n개의 데이터를 비교하며 합침)
merge(arr, left, mid, right);
}
}5. O(n^2) : 2차 시간 (Quadratic Time)
입력값 n의 제곱만큼 시간이 걸리는 경우
주로 중첩 반복문에서 나타난다.
public void print(int[] arr) {
// 바깥 루프 n번 * 안쪽 루프 n번 = n^2
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length; j++) {
System.out.println(arr[i] + ", " + arr[j]);
}
}
}6. O(2^n) : 지수 시간 (Exponential Time)
문제를 해결할 때마다 경우의 수가 2배씩 늘어나는 경우
대표적으로 재귀로 구현한 피보나치 수열이 있다.
public int fibonacci(int n) {
if (n <= 1) return n;
// 호출될 때마다 2개씩 자기 자신을 다시 호출
return fibonacci(n - 1) + fibonacci(n - 2);
}| 잘못된 내용이 있다면 지적부탁드립니다. 방문해주셔서 감사합니다. |

반응형
'Java > Java' 카테고리의 다른 글
| [Java] StringBuilder와 StringBuffer 차이점과 사용법 (0) | 2026.01.16 |
|---|---|
| [Java/알고리즘] 비트 연산자 사용법 (1) | 2026.01.02 |
| [Java] LocalTime , LocalDate의 타입변환 (0) | 2025.12.17 |
| [Java] 자주 사용하는 타입(String, Int, Char) 변환 방법 (0) | 2025.12.02 |
| [Java] 배열, 컬렉션 정렬 방법 (0) | 2025.11.24 |
